


These are the most commonly steps involved in solving word problems in trigonometry. Answer (1 of 2): What I used to do is : 1. In order to master the techniques explained. The remaining 10% is just getting the answer. They are called this because they involve trigonometric functions of double angles, i.e. This is probably the most important trig. Example 1 Use the reciprocal and quotient formulas to verify sectcott csct. Below is an example of a right-angled ABC, using which you can prove these identities. Once the diagram is drawn and we have translated the English Statement (information) given in the question as mathematical equation using trigonometric ratios correctly, 90% of the work will be over. Summary of trigonometric identities sin squared + cos squared 1, The Pythagorean formula for sines and cosines. There are basically three trigonometric identities in the trigonometry chapter. Now we have to use one of the three trigonometric ratios (sin, cos and tan) to find the unknown side or angle. Giving name for the positions would be easier for us to identify the parts of the diagram. All Trigonometry formula class 11th All trigonometric formula & identities class 11 trigonometryTrigonometry Class11Trigonometry IiTJeemaths AllTrig. Once we understand the given information clearly and correct diagram is drawn, solving word problems in trigonometry would not be a challenging work.Īfter having drawn the appropriate diagram based on the given information, we have to give name for each position of the diagram using English alphabets (it is clearly shown in the word problem given below). Drawing diagram for the given information will give us a clear understanding about the question. The diagram we draw for the given information must be correct. We have to draw diagram almost for all of the word problems in trigonometry. Because, when we split the given information in to parts, we can understand them easily. If it is possible, we have to split the given information. Understanding the question and drawing the appropriate diagram are the two most important things to be done in solving word problems in trigonometry. Trigonometric Ratio is known for the relationship between the measurement of the angles and the length of the side of the right triangle. These trigonometry identities are true for all values of the variables. Solving Word Problems Using Trigonometric Identities Trigonometric Identities are some formulas that involve trigonometric functions.
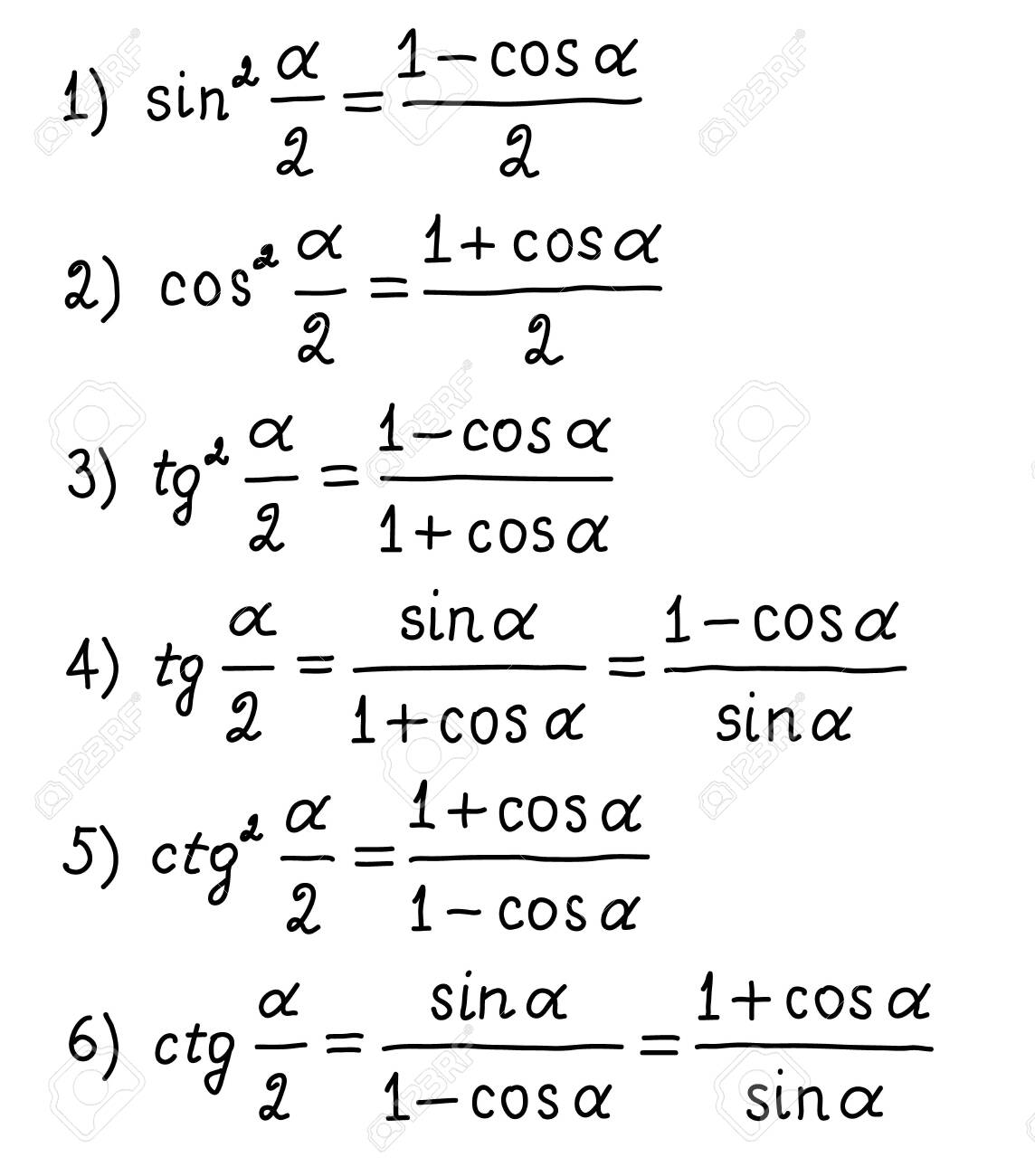
SinC - sinD = 2cossinĬosC + cosD = 2coscosĬosC - cosD = 2sin ⋅ sin Values of Trigonometric Ratios for Standard Angles Tan3A = (3t anA - tan 3 A)/(1 - 3t an 2 A) Sum to Product Identities Tan 2 (A/2) = (1 - cosA)/(1 + cosA) Triple Angle Identities Tan(A - B) = (tanA - tanB)/(1 + tanAtanB) Double Angle IdentitiesĬos 2A = (1 + cos2A)/2 Half Angle IdentitiesĬcosA = /

Tan(A + B) = (tanA + tanB)/(1 - tanAtanB) Section 7.1 Solving Trigonometric Equations and Identities 413 Try it Now 2. Choose one side of the equation to simplify and show that it is equal to the other side. SOHCAHTOAĬotθ = Adjacent side/Opposite side Reciprocal Trigonometric IdentitiesĬotθ = 1/tanθ Other Trigonometric IdentitiesĬot 2θ = csc 2θ - 1 Compound Angles Identities Square identity Change all trigonometric ratios to sine and cosine. Geometrically, these are identities involving certain functions of one or more angles. There are two basic types of trigonometric equations: identities and. "Trigonometric Addition Formulas." From MathWorld-A Wolfram Web Resource.Trigonometric identities are equalities where we would have trigonometric functions and they would be true for every value of the occurring variables. A trigonometric equation is any equation that includes a trigonometric function. On Wolfram|Alpha Trigonometric Addition Formulas Cite this as: A formula for computing the trigonometric identities for the third-angle exists. Without Words: Geometry of Subtraction Formulas." Math. All of the trigonometric functions of an angle can be constructed. CRC Standard Mathematical Tables, 28th ed.


 0 kommentar(er)
0 kommentar(er)
